Question:
In the given figure, the value of x for which DE || AB is
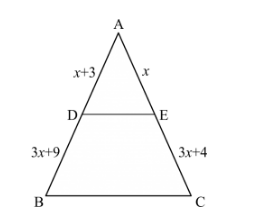
(a) 4
(b) 1
(c) 3
(d) 2
Solution:
Given: In ∆ABC, DE || AB.
To find: the value of x
According to basic proportionality theorem if a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
In ∆ABC, DE || AB
$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$
$\frac{x+3}{3 x+19}=\frac{x}{3 x+4}$
$(x+3)(3 x+4)=(x)(3 x+19)$
$3 x^{2}+4 x+9 x+12=3 x^{2}+19 x$
$19 x-13 x=12$
$6 x=12$
$x=2$
Hence we got the result $(d)$.