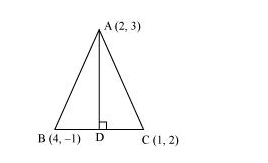
In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2),

Let AD be the altitude of triangle ABC from vertex A.

Accordingly, $A D \perp B C$

The equation of the line passing through point (2, 3) and having a slope of 1 is

(y – 3) = 1(x – 2)

⇒ x – y + 1 = 0

⇒ y – x = 1

Therefore, equation of the altitude from vertex A = y – x = 1.

Length of AD = Length of the perpendicular from A (2, 3) to BC

The equation of BC is

$(y+1)=\frac{2+1}{1-4}(x-4)$

$\Rightarrow(y+1)=-1(x-4)$

$\Rightarrow y+1=-x+4$

$\Rightarrow x+y-3=0$ ..(1)

The perpendicular distance $(d)$ of a line $A x+B y+C=0$ from a point $\left(x_{1}, y_{1}\right)$ is given by $d=\frac{\left|A x_{1}+B y_{1}+C\right|}{\sqrt{A^{2}+B^{2}}}$.

On comparing equation $(1)$ to the general equation of line $A x+B y+C=0$, we obtain $A=1, B=1$, and $C=-3$.

$\therefore$ Length of $A D=\frac{|1 \times 2+1 \times 3-3|}{\sqrt{1^{2}+1^{2}}}$ units $=\frac{|2|}{\sqrt{2}}$ units $=\frac{2}{\sqrt{2}}$ units $=\sqrt{2}$ units

Thus, the equation and the length of the altitude from vertex A are $y-x=1$ and $\sqrt{2}$ units respectively.