In triangle ABC which of the following is not true:
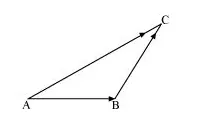
A. $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$
B. $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{AC}}=\overrightarrow{0}$
C. $\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$
D. $\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$
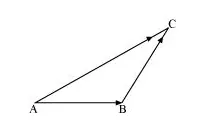
On applying the triangle law of addition in the given triangle, we have:
$\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}$ ...(1)
$\Rightarrow \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=-\overrightarrow{\mathrm{CA}}$
$\Rightarrow \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$ ...(2)
$\therefore$ The equation given in alternative $\mathrm{A}$ is true.
$\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}$
$\Rightarrow \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{AC}}=\overrightarrow{0}$
$\therefore$ The equation given in alternative $B$ is true.
From equation $(2)$, we have:
$\overrightarrow{\mathrm{AB}}-\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$
$\therefore$ The equation given in alternative $\mathrm{D}$ is true.
Now, consider the equation given in alternative $\mathrm{C}$ :
$\overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}-\overrightarrow{\mathrm{CA}}=\overrightarrow{0}$
$\Rightarrow \overrightarrow{\mathrm{AB}}+\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{CA}}$ $\ldots(3)$
From equations (1) and (3), we have:
$\overrightarrow{\mathrm{AC}}=\overrightarrow{\mathrm{CA}}$
$\Rightarrow \overrightarrow{\mathrm{AC}}=-\overrightarrow{\mathrm{AC}}$
$\Rightarrow \overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{AC}}=\overrightarrow{0}$
$\Rightarrow 2 \overrightarrow{\mathrm{AC}}=\overrightarrow{0}$
$\Rightarrow \overrightarrow{\mathrm{AC}}=\overrightarrow{0}$, which is not true.
Hence, the equation given in alternative $C$ is incorrect.
The correct answer is $\mathbf{C}$.
