It is given that ΔABC ~ ΔEDF such that AB = 5 cm,

Given, ΔABC ~ ΔEDF, so the corresponding sides of ΔASC and ΔEDF are in the same ratio.

i.e., $\frac{A B}{E D}=\frac{A C}{E F}=\frac{B C}{D F}$  $\cdots$ (i)

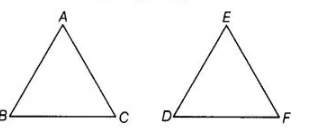
Also, $\quad A B=5 \mathrm{~cm}, A C=7 \mathrm{~cm}$

$D F=15 \mathrm{~cm}$ and $D E=12 \mathrm{~cm}$

On putting these values in Eq. (i), we get

$\frac{5}{12}=\frac{7}{E F}=\frac{B C}{15}$

On taking first and second terms, we get

$\frac{5}{12}=\frac{7}{E F}$

$\Rightarrow$ $E F=\frac{7 \times 12}{5}=16.8 \mathrm{~cm}$

On taking first and third terms, we get

$\frac{5}{12}=\frac{B C}{15}$

$\Rightarrow$ $B C=\frac{5 \times 15}{12}=625 \mathrm{~cm}$

Hence, lengths of the remaining sides of the triangles are EF = 16.8 cm and SC = 625 cm.