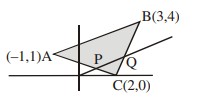
Let $\mathrm{A}(-1,1), \mathrm{B}(3,4)$ and $\mathrm{C}(2,0)$ be given three points. A line $\mathrm{y}=\mathrm{mx}, \mathrm{m}>0$, intersects lines $\mathrm{AC}$ and $\mathrm{BC}$ at point $\mathrm{P}$ and $\mathrm{Q}$ respectively. Let $\mathrm{A}_{1}$ and $\mathrm{A}_{2}$ be the areas of $\triangle \mathrm{ABC}$ and $\triangle \mathrm{PQC}$ respectively, such that $A_{1}=3 A_{2}$, then the value of $m$ is equal to :
Correct Option: , 2
$\mathrm{P} \equiv\left(\mathrm{x}_{1}, \mathrm{mx}_{1}\right)$
$\mathrm{Q} \equiv\left(\mathrm{x}_{2}, \mathrm{mx}_{2}\right)$
$A_{1}=\frac{1}{2}\left|\begin{array}{ccc}3 & 4 & 1 \\ 2 & 0 & 1 \\ -1 & 1 & 1\end{array}\right|=\frac{13}{2}$
$A_{2}=\frac{1}{2}\left|\begin{array}{ccc}x_{1} & m x_{1} & 1 \\ x_{2} & m x_{2} & 1 \\ 2 & 0 & 1\end{array}\right|$
$\mathrm{A}_{2}=\frac{1}{2}\left|2\left(\mathrm{~m} \mathrm{x}_{1}-\mathrm{mx}_{2}\right)\right|=\mathrm{m}\left|\mathrm{x}_{1}-\mathrm{x}_{2}\right|$
$A_{1}=3 A_{2} \Rightarrow \frac{13}{2}=3 m\left|x_{1}-x_{2}\right|$
$\Rightarrow\left|x_{1}-x_{2}\right|=\frac{16}{6 m}$
$A C: x+3 y=2$
$B C: y=4 x-8$
$P: x+3 y=2 \& y=m x \Rightarrow x_{1}=\frac{2}{1+3 m}$
$Q: y=4 x-8 \& y=m x \Rightarrow x_{2}=\frac{8}{4-m}$
$\left|x_{1}-x_{2}\right|=\left|\frac{2}{1+3 m}-\frac{8}{4-m}\right|$
$=\left|\frac{-26 m}{(1+3 m)(4-m)}\right|=\frac{26 m}{(3 m+1)|m-4|}$
$=\frac{26 m}{(3 m+1)(4-m)}$
$\left|x_{1}-x_{2}\right|=\frac{13}{6 m}$
$\frac{26 m}{(3 m+1)(4-m)}=\frac{13}{6 m}$
$\Rightarrow 12 \mathrm{~m}^{2}=-(3 \mathrm{~m}+1)(\mathrm{m}-4)$
$\Rightarrow 12 \mathrm{~m}^{2}=-\left(3 \mathrm{~m}^{2}-11 \mathrm{~m}-4\right)$
$\Rightarrow 15 \mathrm{~m}^{2}-11 \mathrm{~m}-4=0$
$\Rightarrow 15 \mathrm{~m}^{2}-15 \mathrm{~m}+4 \mathrm{~m}-4=0$
$\Rightarrow(15 \mathrm{~m}+4)(\mathrm{m}-1)=0$
$\Rightarrow \mathrm{m}=1$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.