Let A = {1, 2} and B = {2, 4, 6}.

 Given: A = {1, 2} and B = {2, 4, 6}

$f=\{(x, y): x \in A, y \in B$ and $y>2 x+1\}$

Putting x = 1 in y > 2x + 1, we get

$y>2(1)+1$

$\Rightarrow y>3$

and $y \in B$

this means y = 4, 6 if x = 1 because it satisfies the condition y > 3

Putting x = 2 in y > 2x + 1, we get

$y>2(2)+1$

$\Rightarrow y>5$

this means y = 6 if x = 2 because it satisfies the condition y > 5.

∴ f = {(1, 4), (1, 6), (2, 6)}

$(1,2),(2,2),(2,4)$ are not the members of 'f' because they do not satisfy the given condition $y>2 x+1$

Firstly, we have to show that $\mathrm{f}$ is a relation from $\mathrm{A}$ to $\mathrm{B}$.

First elements $=1,2$

All the first elements are in Set A

So, the first element is from set $\mathrm{A}$

Second elements in $F=4,6$

All the second elements are in Set B

So, the second element is from set $B$

Since the first element is from set $A$ and second element is from set $B$

Hence, $F$ is a relation from $A$ to $B$.

Function:

(i) all elements of the first set are associated with the elements of the second set.

(ii) An element of the first set has a unique image in the second set. 

Now, we have to show that f is not a function from A to B

$f=\{(1,4),(1,6),(2,6)\}$

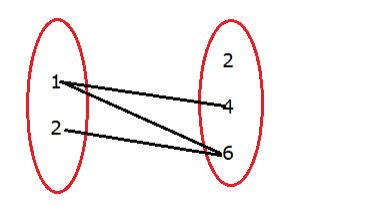
$f=\{(1) 4),(1) 6),(2,6)\}$

Here, 1 is coming twice.

Hence, it does not have a unique (one) image.

So, it is not a function.