Question:
Let A = {2, 4, 6, 8, 10}, B = {4, 8, 12, 16} and C = {6, 12, 18, 24}. Using Venn diagrams, verify that:
(i) $(A \cup B) \cup C=A \cup(B \cup C)$
(ii) $(A \cap B) \cap C=A \cap(B \cap C)$.
Solution:
(i) LHS:
$A^{U} B=\{2,4,6,8,10,12,16\}\left(A^{U} B\right)^{U} C=\{2,4,6,8,10,12,16,18,24\}$
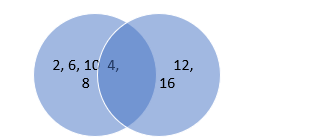
A
B
RHS:
$\mathrm{B}^{U} \mathrm{C}=\{4,6,8,10,12,16,18,24\}$
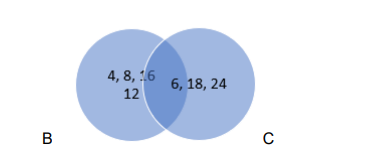
$A^{U}\left(B^{U} C\right)=\{2,4,6,8,10,12,16,18,24\}$
LHS = RHS. [Verified]
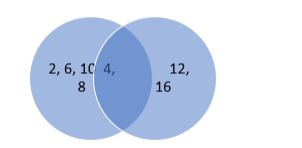
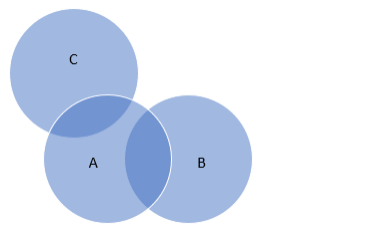
(ii) LHS:
$A^{\cap} B=\{4,8\}\left(A^{\cap} B\right)^{\cap} C=\{\}$ or $\varnothing$
A
B
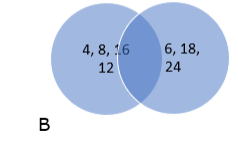
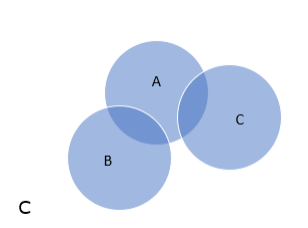
RHS:
$B^{\cap} C=\{12\} A^{\cap}\left(B^{\cap} C\right)=\{\}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
