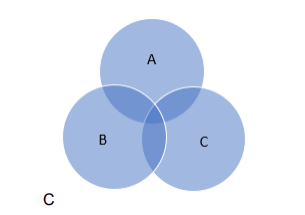
Let A = {a, e, I, o, u}, B = {a, d, e, o, v} and C = {e, o, t, m}. Using Venn diagrams, verify the following
(i) $A \cup(B \cap C)=(A \cup B) \cap(A \cup C)$
(ii) $A \cap(B \cup C)=(A \cap B) \cup(A \cap C)$.
(i) Given:
A = {a, e, I, o, u}, B = {a, d, e, o, v} and C = {e, o, t, m}.
$B^{\cap} C=\{e, o\}$ and $A^{U}\left(B^{\cap} C\right)=\{a, e, I, o, u\}$
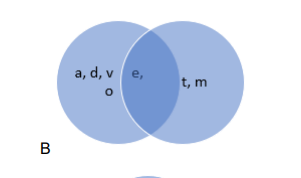
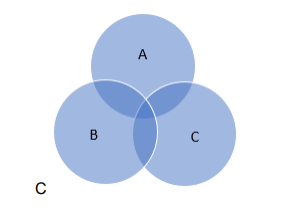
RHS:
$A^{U} B=\{a, d, e, I, o, u, v\}$ and $A^{U} C=\{a, e, I, o, u, t, m\}$
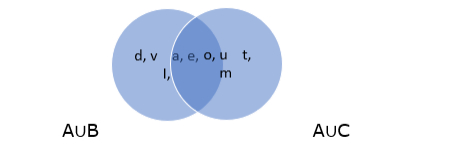
$\left(A^{U} B\right) \cap(A \cup C)=\{a, e, I, o, u\}$
LHS = RHS. [Verified].
(ii) Given:
$A=\{a, e, I, o, u\}, B=\{a, d, e, o, v\}$ and $C=\{e, o, t, m\}$
$\mathrm{B}^{\mathrm{U}} \mathrm{C}=\{\mathrm{a}, \mathrm{d}, \mathrm{v}, \mathrm{e}, \mathrm{o}, \mathrm{t}, \mathrm{m}\}$ and $\mathrm{A}^{\cap}\left(\mathrm{B}^{U} \mathrm{C}\right)=\{\mathrm{a}, \mathrm{e}, \mathrm{o}\}$
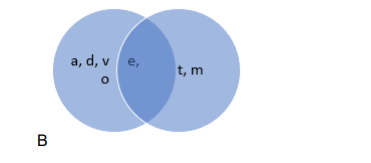
RHS:
$A^{\cap} B=\{a, e, o\}$ and $A^{\cap} C=\{e, o\}$
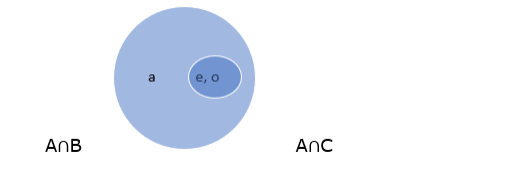
$(A \cap B) \cup(A \cap C)=\{a, e, o\}$
LHS = RHS. [Verified]
