Question:
Let 'a' be a real number such that the function $f(x)=a x^{2}+6 x-15, x \in \mathbf{R}$ is increasing in $\left(-\infty, \frac{3}{4}\right)$ and decreasing in $\left(\frac{3}{4}, \infty\right)$. Then the function $g(x)=a x^{2}-6 x+15, x \in \mathbf{R}$ has a:
Correct Option: 1
Solution:
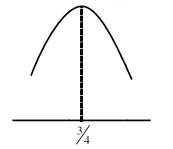
$\frac{-B}{2 A}=\frac{3}{4}$
$\Rightarrow \frac{-(6)}{2 a}=\frac{3}{4}$
$\Rightarrow a=\frac{-6 \times 4}{6} \Rightarrow a=-4$
$\therefore g(x)=4 x^{2}-6 x+15$
Local max. at $\mathrm{x}=\frac{-\mathrm{B}}{2 \mathrm{~A}}=-\frac{(-6)}{2(-4)}$
$=\frac{-3}{4}$
