Question:
Let a function $f:(0, \infty) \rightarrow(0, \infty)$ be defined by
$f(x)=\left|1-\frac{1}{x}\right| .$ Then $f$ is :-
Correct Option: , 2
Solution:
$f(x)=\left|1-\frac{1}{x}\right|=\frac{|x-1|}{x}=\left\{\begin{array}{cc}\frac{1-x}{x} & 0 $\Rightarrow f(x)$ is not injective but range of function is $[0, \infty)$ Remark: If co-domain is $[0, \infty)$, then $f(x)$ will be surjective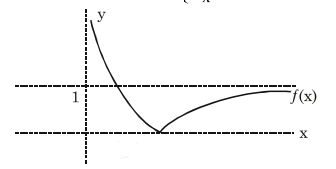
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
