Let $\mathrm{ABC}$ be a triangle with $\mathrm{A}(-3,1)$ and
$\angle \mathrm{ACB}=\theta, 0<\theta<\frac{\pi}{2} .$ If the equation of the median through $\mathrm{B}$ is $2 \mathrm{x}+\mathrm{y}-3=0$ and the equation of angle bisector of $C$ is $7 x-4 y-1=0$, then $\tan \theta$ is equal to:
Correct Option: , 3
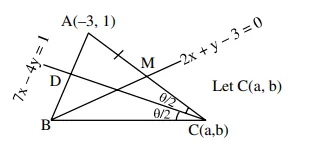
$\therefore \quad M\left(\frac{a-3}{2}, \frac{b+1}{2}\right)$ lies on $2 x+y-3=0$
$\Rightarrow 2 \mathrm{a}+\mathrm{b}=11$ .....(i)
$\because$ C lies on $7 \mathrm{x}-4 \mathrm{y}=1$
$\Rightarrow 7 \mathrm{a}-4 \mathrm{~b}=1$ ....(ii)
$\therefore$ by (i) and (ii) : $\mathrm{a}=3, \mathrm{~b}=5$
$\Rightarrow \mathrm{C}(3,5)$
$\therefore \mathrm{m}_{A C}=2 / 3$
Also, $\mathrm{m}_{\mathrm{CD}}=7 / 4$
$\Rightarrow \tan \frac{\theta}{2}=\left|\frac{\frac{2}{3}-\frac{4}{4}}{1+\frac{14}{12}}\right| \Rightarrow \tan \frac{\theta}{2}=\frac{1}{2}$
$\Rightarrow \tan \theta=\frac{2 \cdot \frac{1}{2}}{1-\frac{1}{4}}=\frac{4}{3}$
