Let $\mathrm{ABCD}$ be a square of side of unit length.
Let a circle $C_{1}$ centered at $A$ with unit radius is drawn. Another circle $C_{2}$ which touches $C_{1}$ and the lines $\mathrm{AD}$ and $\mathrm{AB}$ are tangent to it, is also drawn. Let a tangent line from the point $\mathrm{C}$ to the circle $\mathrm{C}_{2}$ meet the side $\mathrm{AB}$ at $\mathrm{E}$.
If the length of EB is $\alpha+\sqrt{3} \beta$, where $\alpha, \beta$ are integers 8 then $\alpha+\beta$ is equal to_______.
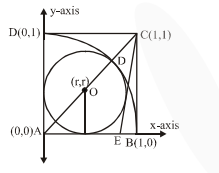
Here $\mathrm{AO}+\mathrm{OD}=1$ or $(\sqrt{2}+1) \mathrm{r}=1$
$\Rightarrow \quad \mathrm{r}=\sqrt{2-1}$
equation of circle $(x-r)^{2}+(y-r)^{2}=r^{2}$ Equation of CE
Equation of CE
$y-1=m(x-1)$
$m x-y+1-M=0$
It is tangent to circle
$\therefore \quad\left|\frac{\mathrm{mr}-\mathrm{r}+1-\mathrm{m}}{\sqrt{\mathrm{m}^{2}+1}}\right|=\mathrm{r}$
$\left|\frac{(\mathrm{m}-1) \mathrm{r}+1-\mathrm{m}}{\sqrt{\mathrm{m}^{2}+1}}\right|=\mathrm{r}$
$\frac{(m-1)^{2}(r-1)^{2}}{m^{2}+1}=r^{2}$
Put $r=\sqrt{2}-1$
On solving $m=2-\sqrt{3}, 2+\sqrt{3}$
Taking greater slope of $\mathrm{CE}$ as
$2+\sqrt{3}$
$y-1=(2+\sqrt{3})(x-1)$
Put $\quad y=0$
$-1=(2+\sqrt{3})(x-1)$
$\frac{-1}{2+\sqrt{3}} \times\left(\frac{2-\sqrt{3}}{2-\sqrt{3}}\right)=x-1$
$x-1=\sqrt{3}-1$
$\mathrm{EB}=1-\mathrm{x}=1-(\sqrt{3}-1)$
$\mathrm{EB}=2-\sqrt{3}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
