Let $f: R \rightarrow R$ and $g: R \rightarrow R$ be defined as
$f(x)=\left\{\begin{array}{cc}x+a, & x<0 \\ |x-1|, & x \geq 0\end{array}\right.$ and
$g(x)=\left\{\begin{array}{cc}x+1, & x<0 \\ (x-1)^{2}+b, & x \geq 0\end{array}\right.$
where $a, b$ are non-negative real numbers. If (gof) $(\mathrm{x})$ is continuous for all $\mathrm{x} \in \mathrm{R}$, then $\mathrm{a}+\mathrm{b}$ is equal to_________.
$g[f(x)]=\left[\begin{array}{cc}f(x)+1 & f(x)<0 \\ (f(x)-1)^{2}+b & f(x) \geq 0\end{array}\right.$
$\mathrm{g}[\mathrm{f}(\mathrm{x})]=\left[\begin{array}{cc}\mathrm{x}+\mathrm{a}+1 & \mathrm{x}+\mathrm{a}<0 \& \mathrm{x}<0 \\ |\mathrm{x}-1|+1 & |\mathrm{x}-1|<0 \& \mathrm{x} \geq 0 \\ (\mathrm{x}+\mathrm{a}-1)^{2}+\mathrm{b} & \mathrm{x}+\mathrm{a} \geq 0 \& \mathrm{x}<0 \\ (|\mathrm{x}-1|-1)^{2}+\mathrm{b} & |\mathrm{x}-1| \geq 0 \& \mathrm{x} \geq 0\end{array}\right.$
$\mathrm{g}[\mathrm{f}(\mathrm{x})]=\left[\begin{array}{cc}\mathrm{x}+\mathrm{a}+1 & \mathrm{x} \in(-\infty,-\mathrm{a}) \& \mathrm{x} \in(-\infty, 0) \\ |\mathrm{x}-1|+1 & \mathrm{x} \in \phi \\ (\mathrm{x}+\mathrm{a}-1)^{2}+\mathrm{b} & \mathrm{x} \in[-\mathrm{a}, \infty) \& \mathrm{x} \in(-\infty, 0) \\ (|\mathrm{x}-1|-1)^{2}+\mathrm{b} & \mathrm{x} \in \mathrm{R} \& \mathrm{x} \in[0, \infty)\end{array}\right.$
$\mathrm{g}[\mathrm{f}(\mathrm{x})]=\left[\begin{array}{cc}\mathrm{x}+\mathrm{a}+1 & \mathrm{x} \in(-\infty,-\mathrm{a}) \\ (\mathrm{x}+\mathrm{a}-1)^{2}+\mathrm{b} & \mathrm{x} \in[-\mathrm{a}, 0) \\ (|\mathrm{x}-1|-1)^{2}+\mathrm{b} & \mathrm{x} \in[0, \infty)\end{array}\right.$
$g(f(x))$ is continuous
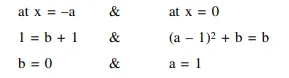
$\Rightarrow \quad a+b=1$
