Let f: W → W be defined as f(n) = n − 1, if is odd and f(n) = n + 1,

It is given that:

$f: W \rightarrow W$ is defined as $f(n)= \begin{cases}n-1, & \text { if } n \text { is odd } \\ n+1, & \text { if } n \text { is even }\end{cases}$

One-one:

Let f(n) = f(m).

It can be observed that if n is odd and m is even, then we will have n − 1 = m + 1.

$\Rightarrow n-m=2$

However, this is impossible.

Similarly, the possibility of n being even and m being odd can also be ignored under a similar argument.

∴Both n and m must be either odd or even.

Now, if both n and m are odd, then we have:

$f(n)=f(m) \Rightarrow n-1=m-1 \Rightarrow n=m$

Again, if both $n$ and $m$ are even, then we have:

f(n) = f(m) ⇒ n + 1 = m + 1 ⇒ n = m

∴f is one-one.

It is clear that any odd number $2 r+1$ in co-domain $\mathbf{N}$ is the image of $2 r$ in domain $\mathbf{N}$ and any even number $2 r$ in co-domain $\mathbf{N}$ is the image of $2 r+1$ in domain $\mathbf{N}$.

=∴f is onto.

Hence, f is an invertible function.

Let us define $g: W \rightarrow W$ as:

$g(m)=\left\{\begin{array}{l}m+1, \text { if } m \text { is even } \\ m-1, \text { if } m \text { is odd }\end{array}\right.$

Now, when n is odd:

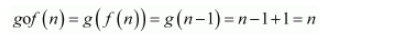
And, when n is even:

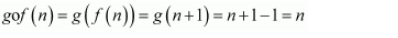
Similarly, when m is odd:

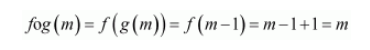
When m is even:

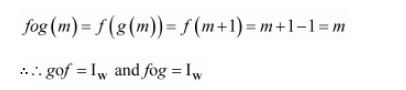
Thus, $f$ is invertible and the inverse of $f$ is given by $f^{-1}=g$, which is the same as $f$.

Hence, the inverse of $f$ is $f$ itself.