Let f(x) be a polynomial of degree 5 such that

$f(x)=a x^{5}+b x^{4}+c x^{3}$

$\lim _{x \rightarrow 0}\left(2+\frac{a x^{5}+b x^{4}+c x^{3}}{x^{3}}\right)=4$

$\Rightarrow 2+c=4 \Rightarrow c=2$

$f^{\prime}(x)=5 a x^{4}+4 b x^{3}+6 x^{2}$

$=x^{2}\left(5 a x^{2}+4 b x+6\right)$

Since, $x=\pm 1$ are the critical points,

$\therefore \quad f^{\prime}(1)=0 \Rightarrow 5 a+4 b+6=0$ ...(1)

$f^{\prime}(-1)=0 \Rightarrow 5 a-4 b+6=0$......(2)

From eqns. (1) and (2),

$b=0$ and $a=-\frac{6}{5}$

$f(x)=\frac{-6}{5} x^{5}+2 x^{3}$

$f^{\prime}(x)=-6 x^{4}+6 x^{2}=6 x^{2}\left(-x^{2}+1\right)$

$=-6 x^{2}(x+1)(x-1)$

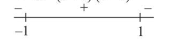
$\therefore f(x)$ has minima at $x=-1$ and maxima at $x=1$