Question:
Let $[\mathrm{t}]$ denote the greatest integer $\leq \mathrm{t}$. Then the
value of $8 \cdot \int_{-\frac{1}{2}}^{1}([2 x]+|x|) d x$ is__________.
Solution:
$I=\int_{-1 / 2}^{1}([2 x]+|x|) d x$
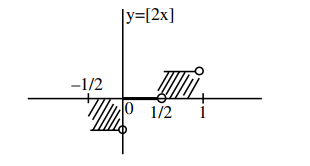
$=\int_{-1 / 2}^{1}[2 x] d x+\int_{-1 / 2}^{1}|x| d x$
$=0+\int_{-1 / 2}^{0}(-x) d x+\int_{0}^{1} x d x$
$=\left(-\frac{x^{2}}{2}\right)_{-1 / 2}^{0}+\left(\frac{x^{2}}{2}\right)_{0}^{1}$
$=\left(0+\frac{1}{8}\right)+\frac{1}{2}$
$=\frac{5}{8}$
$8 I=5$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
