Question:
Let the centroid of an equilateral triangle $\mathrm{ABC}$ be at the origin. Let one of the sides of the equilateral triangle be along the straight line $x+y=3$. If $R$ and $r$ be the radius of circumcircle and incircle respectively of $\Delta \mathrm{ABC}$, then $(\mathrm{R}+\mathrm{r})$ is equal to:
Correct Option: 1
Solution:
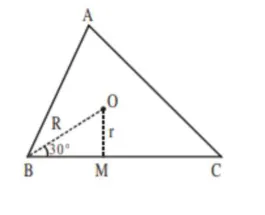
$r=O M=\frac{3}{\sqrt{2}}$
$\& \sin 30^{\circ}=\frac{1}{2}=\frac{r}{R} \Rightarrow R=\frac{6}{\sqrt{2}}$
$\therefore r+R=\frac{9}{\sqrt{2}}$
