Question:
Let the latus ractum of the parabola $y^{2}=4 x$ be the common chord to the circles $C_{1}$ and $C_{2}$ each
of them having radius $2 \sqrt{5}$. Then, the distance
between the centres of the circles $\mathrm{C}_{1}$ and $\mathrm{C}_{2}$ is:
Correct Option: 1,
Solution:
Length of latus rectum $=4$
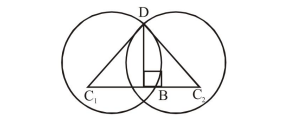
$\mathrm{DB}=2$
$C_{1} B=\sqrt{\left(C_{1} D\right)^{2}-(D B)^{2}}=4$
$\mathrm{C}_{1} \mathrm{C}_{2}=8$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.