Question:
Let the normals at all the points on a given curve pass through a fixed point $(a, b)$. If the curve passes through $(3,-3)$ and $(4,-2 \sqrt{2})$, and given that $a-2 \sqrt{2} b=3$, then $\left(a^{2}+b^{2}+a b\right)$ is equal to
Solution:
All normals of circle passes through centre
Radius $=\mathrm{CA}=\mathrm{CB}$
$\mathrm{CA}^{2}=\mathrm{CB}^{2}$
$(a-3)^{2}+(b+3)^{2}$
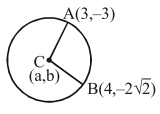
$=(a-4)^{2}+(b-2 \sqrt{2})^{2}$
$a+(3-2 \sqrt{2}) b=3$
$a-2 \sqrt{2} b+3 b=3$...(1)
given that $a-2 \sqrt{2} b=3$...(2)
from (1) \& (2) $\Rightarrow a=3, b=0$
$a^{2}+b^{2}+a b=9$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
