Let $f: \mathbf{R}-\left\{-\frac{4}{3}\right\} \rightarrow \mathbf{R}$ be a function defined as $f(x)=\frac{4 x}{3 x+4}$. The inverse of $f$ is map $g$ : Range $f \rightarrow \mathbf{R}-\left\{-\frac{4}{3}\right\}$ given by
(A) $g(y)=\frac{3 y}{3-4 y}$
(B) $g(y)=\frac{4 y}{4-3 y}$
(C) $g(y)=\frac{4 y}{3-4 v}$
(D) $g(y)=\frac{3 y}{4-3 y}$
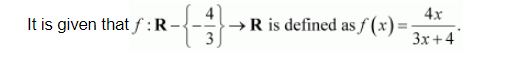
Let $y$ be an arbitrary element of Range $f$.
Then, there exists $x \in \mathbf{R}-\left\{-\frac{4}{3}\right\}$ such that $y=f(x)$.
$\Rightarrow y=\frac{4 x}{3 x+4}$
$\Rightarrow 3 x y+4 y=4 x$ Let us define g: Range![]() as
as![]()
$\Rightarrow x(4-3 y)=4 y$
$\Rightarrow x=\frac{4 y}{4-3 y}$ Now,![]()
$=\frac{4\left(\frac{4 x}{3 x+4}\right)}{4-3\left(\frac{4 x}{3 x+4}\right)}=\frac{16 x}{12 x+16-12 x}=\frac{16 x}{16}=x$
And, $(f \circ g)(y)=f(g(y))=f\left(\frac{4 y}{4-3 y}\right)$
$=\frac{4\left(\frac{4 y}{4-3 y}\right)}{3\left(\frac{4 y}{4-3 y}\right)+4}=\frac{16 y}{12 y+16-12 y}=\frac{16 y}{16}=y$
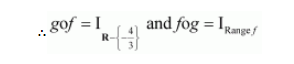
Thus, $g$ is the inverse of $f$ i.e., $f^{-1}=g$.
Hence, the inverse of $f$ is the map $g$ : Range $f \rightarrow \mathbf{R}-\left\{-\frac{4}{3}\right\}$, which is given by
$g(y)=\frac{4 y}{4-3 y}$
The correct answer is B.
