Question:
Mark (√) against the correct answer in the following
$f: C \rightarrow R: f(z)=|z|$ is
A. one - one and into
B. one - one and onto
C. many - one and into
D. many - one and onto
Solution:
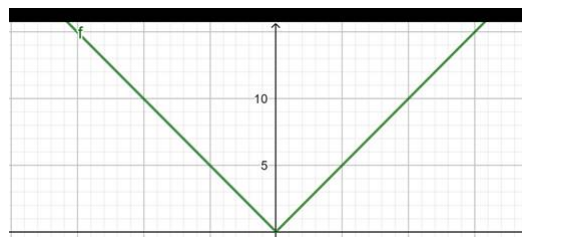
Here in this range the lines cut the curve in 2 equal valued points of $y$ therefore the function $f(z)=|z|$ is not one - one
$\Rightarrow f(z)=$ many one
Range of $f(z)=[0, \infty) \neq R$ (codomain)
$\therefore f(z)$ is not onto.
$\Rightarrow f(z)=$ into
Hence, $f(z)=|z|$ is many one and into
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.