Question:
Mark (√) against the correct answer in the following:
Let $f(x)=\frac{\sin ^{-1} x}{x} .$ Then, dom $(f)=?$
A. $(-1,1)$
B. $[-1,1]$
C. $[-1,1]-\{0\}$
D. none of these
Solution:
Given: $f(x)=\frac{\sin ^{-1} x}{x}$
From f(x), x ≠ 0
Now, domain of $\sin ^{-1} x$ is $[-1,1]$ as the values of $\sin ^{-1} x$ lies between $-1$ and 1 .
We can see that from this graph:
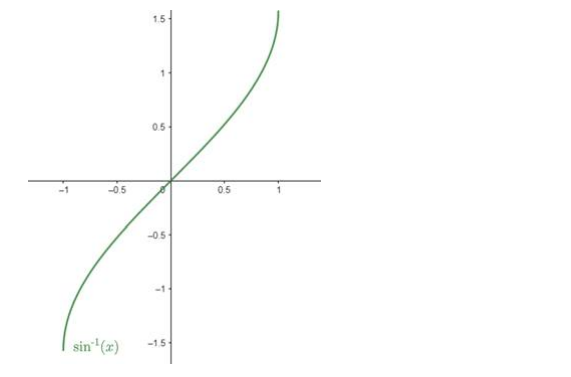
Domain of $f(x)=[-1,1]-0$
Hence, B is the correct answer.
