Mark the correct alternative in each of the following:
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) $\sqrt{119} \mathrm{~cm}$
Let us first put the given data in the form of a diagram.
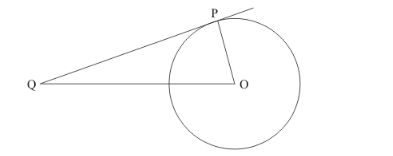
Given data is as follows:
OQ = 12 cm
OP = 5 cm
We have to find the length of QP.
We know that the radius of a circle will always be perpendicular to the tangent at the point of contact. Therefore, OP is perpendicular to QP. We can now use Pythagoras theorem to find the length of QP.
$Q P^{2}=O Q^{2}-O P^{2}$
$Q P^{2}=12^{2}-5^{2}$
$Q P^{2}=144-25$
$Q P^{2}=119$
$Q P=\sqrt{119}$
Therefore the correct answer is choice (d).
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.