Mark the tick against the correct answer in the following:

To Find: The range of $\tan ^{-1} \mathrm{x}$

Here,the inverse function is given by $y=f^{-1}(x)$

The graph of the function $y=\tan ^{-1}(x)$ can be obtained from the graph of

$Y=\tan x$ by interchanging $x$ and $y$ axes.i.e, if $(a, b)$ is a point on $Y=\tan x$ then $(b, a)$ is the point on the function $y=\tan ^{-1}(x)$

Below is the Graph of the range of $\tan ^{-1}(x)$

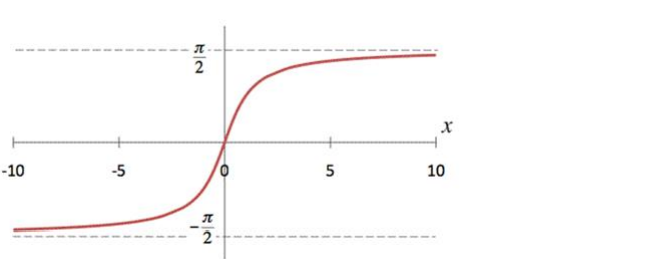
From the graph, it is clear that the range of $\tan ^{-1}(x)$ is restricted to any of the intervals like $\left[-\frac{3 \pi}{2},-\frac{\pi}{2}\right],[$ $\left.-\frac{\pi}{2}, \frac{\pi}{2}\right],\left[\frac{\pi}{2}, \frac{3 \pi}{2}\right]$ and so on. Hence the range is given by

$\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)$