Match the following columns:

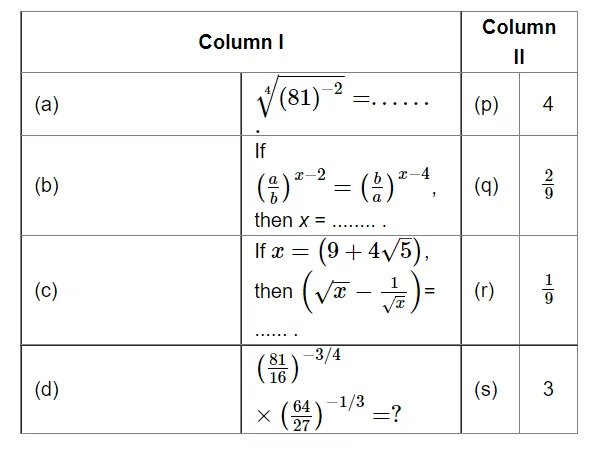
(a)

$\left((81)^{-2}\right)^{\frac{1}{4}}$

$=\left((9)^{-4}\right)^{\frac{1}{4}}=(9)^{-4 \times \frac{1}{4}}=(9)^{-1}$

$=\frac{1}{9}$

$=\frac{1}{9}$

(b)

$\left(\frac{a}{b}\right)^{x-2}=\left(\frac{b}{a}\right)^{x-4}$

$\Rightarrow\left(\frac{b}{a}\right)^{2-x}=\left(\frac{b}{a}\right)^{x-4}$

$\Rightarrow 2-x=x-4$

$\Rightarrow 2 x=6$

$\Rightarrow x=3$

(c)

$x=9+4 \sqrt{5}$

and

$\frac{1}{x}=\frac{1}{9+4 \sqrt{5}} \times \frac{9-4 \sqrt{5}}{9-4 \sqrt{5}}$

$=\frac{9-4 \sqrt{5}}{81-80}$

$=9-4 \sqrt{5}$

Now,

$x+\frac{1}{x}=9+4 \sqrt{5}+9-4 \sqrt{5}=18$

Thus, we have :

$x+\frac{1}{x}=18$

We know :

$\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2}=x+\frac{1}{x}-2 \times x \times \frac{1}{x}$

$\Rightarrow\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2}=18-2$

$\Rightarrow\left(\sqrt{x}-\frac{1}{\sqrt{x}}\right)^{2}=16$

Taking the square root of both sides, we get:

$\sqrt{x}-\frac{1}{\sqrt{x}}=4$

(d)

$\left(\frac{3}{2}\right)^{4 \times \frac{-3}{4}} \times\left(\frac{4}{3}\right)^{3 \times \frac{-1}{3}}$

$=\left(\frac{3}{2}\right)^{-3} \times\left(\frac{4}{3}\right)^{-1}$

$=\left(\frac{3}{2}\right)^{-3} \times \frac{3}{4}$

$=\left(\frac{3^{-3}}{2^{-3}}\right) \times \frac{3}{2^{2}}$

$=\left(\frac{3^{-3} \times 3}{2^{-3} \times 2^{2}}\right)$

$=\frac{3^{-2}}{2^{-1}}$

$=\frac{2}{9}$