Match the following figures:

(a)The given figure is a cuboid with sides 4,4 and 6 units.Area of a rectangle $=$ length $\times$ width $\therefore$ Area of the rectangular face sith sides 4 and $4=4 \times 4=16$ And, area of the other face with sides

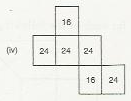
(b) The given figure is a cuboid with sides 3,3 and 8 .

Area of a rectangle $=$ length $\times$ width

$\therefore$ Area of the rectangular face sith sides 3 and $3=3 \times 3=9$

And the area of the other face with sides 3 and $8=3 \times 8=24$

Thus, the net for given figure will have four faces with area 24 and two faces with area 9 .

Observe that net (i) satisfies this.

Thus, the net of figure (b) is net (i).

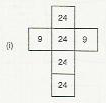
(c) The given figure is a cuboid with sides 3,4 and 6 .

Area of a rectangle $=$ length $\times$ width

$\therefore$ Area of the rectangular face sith sides 3 and $4=3 \times 4=12$,

Area of the rectangular face with sides 4 and $6=4 \times 6=24$

And, area of the other face with sides 3 and $6=3 \times 6=18$

Thus, the net for given figure will have two faces with area 24 , two faces with area 18 and two faces with area 12 .

Observe that net (ii) satisfies this.

Thus, the net of figure (c) is net (ii).

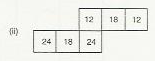
(d) The given figure is a cuboid with sides 3,3 and 9 .

Area of a rectangle $=$ length $\times$ width

Area of the rectangular face with sides 3 and $3=3 \times 3=9$,

And, area of the other face with sides 3 and $9=3 \times 9=27$

Thus, the net for given figure will have four faces with area 27 and two faces with area 9 .

Observe that net (iii) satisfies this.

Thus, the net of figure (d) is net (iii).