Question:
The value of $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(x^{3}+x \cos x+\tan ^{5} x+1\right) d x$ is
A. 0
B. 2
C. $\pi$
D. 1
Solution:
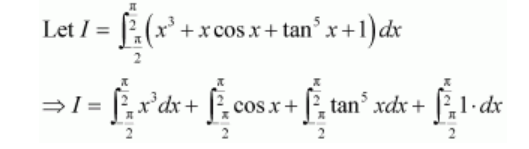
It is known that if $f(x)$ is an even function, then $\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x$ and
if f(x) is an odd function, then $\int_{-a}^{a} f(x) d x=0$
$I=0+0+0+2 \int_{0}^{\pi} 2^{2} 1 \cdot d x$
$=2[x]_{0}^{\frac{\pi}{2}}$
$=\frac{2 \pi}{2}$
$\pi$
Hence, the correct answer is C.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
