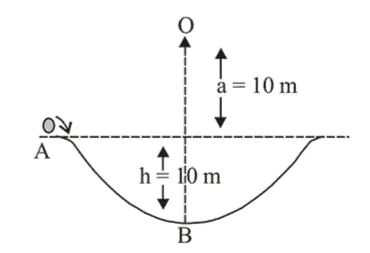
A particle of mass $20 \mathrm{~g}$ is released with an initial velocity $5 \mathrm{~m} / \mathrm{s}$ along the curve from the point $\mathrm{A}$, as shown in the figure. The point $\mathrm{A}$ is at height $\mathrm{h}$ from point $\mathrm{B}$. The particle slides along the frictionless surface. When the particle reaches point $\mathrm{B}$, its angular momentum about $\mathrm{O}$ will be : (Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ )
Correct Option:
(3) According to work-energy theorem
$\mathrm{mgh}=\frac{1}{2} \mathrm{mv}_{\mathrm{B}}^{2}-\frac{1}{2} \mathrm{mv}_{\mathrm{A}}^{2}$
$2 g h=v_{B}^{2}-v_{A}^{2}$
$2 \times 10 \times 10=\mathrm{v}_{\mathrm{B}}^{2}-5^{2}$
$\Rightarrow v_{B}=15 \mathrm{~m} / \mathrm{s}$
Angular momentum about $O$,
$\begin{aligned} L_{O} &=m v r \\ &=20 \times 10^{-3} \times 20 \\ L_{O} &=6 \mathrm{~kg} \cdot \mathrm{m}^{2} / \mathrm{s} \end{aligned}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.