Let L be the line of intersection of planes

$P_{1}: x-y+2 z=2$

$P_{2}=2 x+y-3=2$

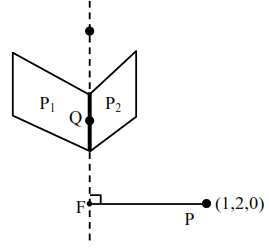
Let line of Intersection of planes $P_{1}$ and $P_{2}$ cuts $x y$ plane in point $Q$.

$\Rightarrow \mathrm{z}-$ coordinate of point $\mathrm{Q}$ is zero

$\left.\Rightarrow \quad \begin{array}{r}x-y=2 \\ \text { and } 2 x+y=2\end{array}\right\} \Rightarrow x=\frac{4}{3}, y=\frac{-2}{3}$

$\Rightarrow Q\left(\frac{4}{3}, \frac{-2}{3}, 0\right)$

Vector parallel to the line of intersection

$\overrightarrow{\mathrm{a}}=\left|\begin{array}{rrr}\hat{\mathrm{i}} & \hat{\mathrm{j}} & \hat{\mathrm{k}} \\ 1 & -1 & 2 \\ 2 & 1 & -1\end{array}\right|=-\hat{\mathrm{i}}+5 \hat{\mathrm{j}}+3 \hat{\mathrm{k}}$

Equation of Line of intersection

$\frac{x-\frac{4}{3}}{-1}=\frac{y+\frac{2}{3}}{5}=\frac{z-0}{3}=\lambda($ say $)$

Let coordinates of foot of perpendicular be

$\mathrm{F}\left(-\lambda+\frac{4}{3}, 5 \lambda-\frac{2}{3}, 3 \lambda\right)$

$\overrightarrow{\mathrm{PF}}=\left(-\lambda+\frac{1}{3}\right) \hat{\mathrm{i}}+\left(5 \lambda-\frac{8}{3}\right) \hat{\mathrm{j}}+(3 \lambda) \hat{\mathrm{k}}$

$\overrightarrow{\mathrm{PF}} \cdot \overrightarrow{\mathrm{a}}=0$

$\Rightarrow \lambda-\frac{1}{3}+25 \lambda \frac{-40}{3}+9 \lambda=0$

$\Rightarrow 35 \lambda=\frac{41}{3} \Rightarrow \lambda=\frac{41}{105}$

Now, $\alpha=-\lambda+\frac{4}{3}, \beta=5 \lambda-\frac{2}{3}, \gamma=3 \lambda$

$\Rightarrow \alpha+\beta+\gamma=7 \lambda+\frac{2}{3}$

$=7\left(\frac{41}{105}\right)+\frac{2}{3}$

$=\frac{51}{15}$

$\Rightarrow 35(\alpha+\beta+\gamma)=\frac{51}{15} \times 35=119$