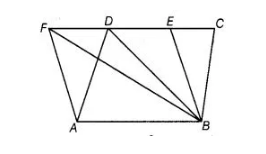
The area of the parallelogram ABCD is

Given, area of parallelogram, ABCD = 90 cm2.

1. We know that, parallelograms on the same base and between the same parallel are equal in areas.
   Here, parallelograms ABCD and ABEF are on same base AB and between the same parallels AB and CF.
   So, ar (ΔBEF) = ar (ABCD) = 90 cm2
2. We know that, if a triangle and a parallelogram are on the same base and between the same parallels, then area of triangle is equal to half of the area of the parallelogram.
   Here, ΔABD and parallelogram ABCD are on the same base AB and between the same parallels AB and CD.
   So, ar (ΔABD) = ½ ar (ABCD)
   = ½ x 90 = 45 cm2 [∴ ar (ABCD) = 90 cm2]
3. Here, ABEF and parallelogram ABEF are on the same base EF and between the same parallels AB and EF.
   ar (ΔBEF) = ½ ar (ABEF)
   = ½ x 90 = 45 cm2 [∴ ar (ABEF) = 90 cm2, from part (i)]