E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersects BC at F. Show thatf is the mid-
point of BC.
Thinking Process
Use the mid-point theorem i.e., the line segment joining the mid-points of two sides of a triangle is parallel to the third side and half of it. Further
shown the required result.
Given ABCD is a trapezium in which AB || DC and EF||AB|| CD.
Construction Join, the diagonal AC which intersects EF at O.
To show F is the mid-point of BC.
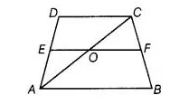
Proof Now, in ΔADC, E is the mid-point of AD and OE || CD. Thus, by mid-point theorem, O is mid-point of AC.
Now, in ΔCBA, 0 is the mid-point of AC and OF || AB.
So, by mid-point theorem, F is the mid-point of BC.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
