Question:
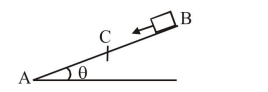
A small block starts slipping down from a point $\mathrm{B}$ on an inclined plane $\mathrm{AB}$, which is making an angle $\theta$ with the horizontal section BC is smooth and the remaining section CA is rough with a coefficient of friction $\mu$. It is found that the block comes to rest as it reaches the bottom (point $\mathrm{A}$ ) of the inclined plane. If $\mathrm{BC}=2 \mathrm{AC}$, the coefficient of friction is given by $\mu=\mathrm{k} \tan \theta$ ). The value of $\mathrm{k}$ is
Solution:
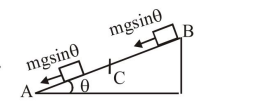
Apply work energy theorem
$m g \sin \theta(A C+2 A C)-\mu m g \cos \theta A C=0$
$\mu=3 \tan \theta$
