n figure, ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that ar (ABCDE) = ar (ΔAPQ).
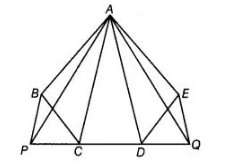
Given ABCDE is a pentagon.
BP || AC and EQ|| AD.
To prove ar (ABCDE) = ar (APQ)
Proof We know that, triangles on the same base and between the same parallels are equal in area.
Here, ΔADQ and ΔADE lie on the same base AD and between the same parallels AD and EQ.
So, ar (ΔADQ) = ar (ΔADE) ...(i)
Similarly, ΔACP and ΔACB lie on the same base AC and between the same parallels AC and BP.
So, ar (ΔACP) = ar (ΔACB) …(ii)
On adding Eqs. (i) and (ii), we get
ar (ΔADQ) + ar (ΔACP) = ar (ΔADE) + ar (ΔACB)
On adding ar (ΔACD) both sides, we get
ar (ΔADQ) + ar (ΔACP) + ar (ΔACD) = ar (ΔADE) + ar (ΔACB) + ar (ΔACD)
=> ar (ΔAPQ) = ar (ABCDE) Hence proved.