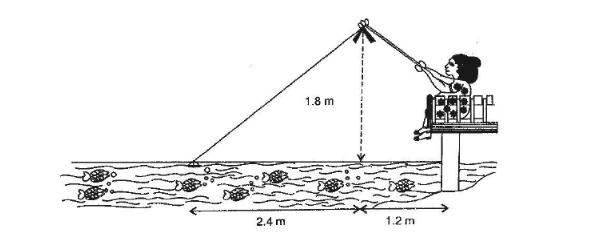
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the road. Assuming that her string (from the tip of her road to the fly) is taut, how much string does she have out (in the given figure)? If she pulls the string at the rate of 5 cm per second, what will the horizontal distance of the fly from her after 12 seconds.
Let us take
AB = Tip of fishing rod above the surface of the water
BC = The string rest from directly under the tip of the rod.
AC = The length of string
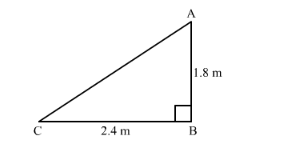
In ABC right triangle right angled at B
$A C^{2}=A B^{2}+B C^{2}$
$A C^{2}=1.8^{2}+2.4^{2}$
$A C^{2}=3.24+5.76$
$A C^{2}=9$
$A C=\sqrt{9}$
$A C=\sqrt{3 \times 3}$
$A C=3$
Hence 3 m string is out
The string pulled in 12 seconds is equal to $12 \times 5=60 \mathrm{~cm}=0.6 \mathrm{~m}$ to point $D$
In this case the diagram will look like the following
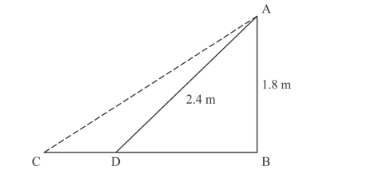
Now The length of the new string AD = AC − CD = 3.00 − 0.6 = 2.4 m
Now in triangle ADB we have
$1.8^{2}+B D^{2}=2.4^{2}$
$3.24+B D^{2}=5.76$
$B D^{2}=5.76-3.24$
$B D^{2}=2.52$
$B D=1.587$
$\therefore$ Required distance $=1.587+1.2=2.79 \mathrm{~m}$
Hence, the horizontal distance is $2.79 \mathrm{~m}$.