O is any point in the interior of ΔABC. Prove that

Given that O is any point in the interior of ΔABC

To prove

(i) AB + AC > OB + OC

(ii) AB + BC + CA > OA + QB + OC

(iii) OA + OB + OC > (1/2)(AB + BC +CA)

We know that in a triangle the sum of any two sides is greater than the third side.

So, we have

In Δ ABC

AB + BC > AC

BC + AC > AB

AC + AB > BC

In ΔOBC

OB + OC > BC ... (i)

In ΔOAC

OA + OC > AC ... (ii)

In ΔOAB

OA + OB > AB ... (iii)

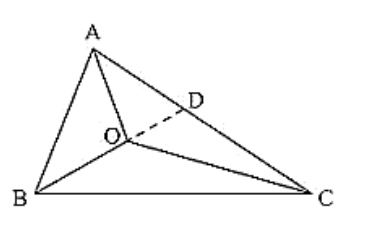
Now, extend (or) produce BO to meet AC in D.

Now, in ΔABD, we have

AB + AD > BD

AB + AD > BO + OD ... (iv)  [BD = BO + OD]

Similarly in ΔODC, we have

OD + DC > OC ... (v)

(i) Adding (iv) and (v), we get

AB + AD + OD + DC > BO + OD + OC

AB + (AD + DC) > OB + OC

AB + AC > OB + OC ... (vi)

Similarly, we have

BC + BA > OA + OC ... (vii)

and CA+ CB > OA + OB ... (viii)

(ii) Adding equation (vi), (vii) and (viii), we get

AB + AC + BC + BA + CA + CB > OB + OC + OA + OC + OA + OB

⟹ 2AB + 2BC + 2CA > 2OA + 2OB + 2OC

⟹ 2(AB + BC + CA) > 2(OA + OB + OC)

⟹ AB + BC + CA > OA + OB + OC

(iii) Adding equations (i), (ii) and (iii)

OB + OC + OA + OC + OA + OB > BC + AC + AB

2OA + 2OB + 2OC > AB + BC + CA

We get = 2(OA + OB + OC) > AB + BC +CA

(OA + OB + OC) > (1/2)(AB + BC +CA)