O is any point on the diagonal PR

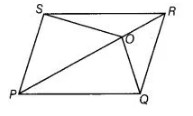
Given in a parallelogram $P Q R S, O$ is any point on the diagonal $P R$.

To prove $\operatorname{ar}(\Delta P S O)=\operatorname{ar}(\triangle P Q O)$

Construction Join $S Q$ which intersects $P R$ at $B$.

Proof We know that, diagonals of a parallelogram bisect each other, so $B$ is the mid-point of $S Q$.

Here, $P B$ is a median of $\triangle Q P S$ and we know that, a median of a triangle divides it into two triangles of equal area.

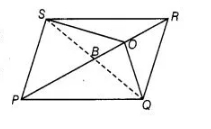
$\therefore$ ar $(\Delta B P Q)=\operatorname{ar}(\triangle B P S)$ $\ldots$ (i)

Also, $O B$ is the median of $\triangle O S Q$.

$\therefore \quad \operatorname{ar}(\Delta O B Q)=\operatorname{ar}(\Delta O B S)$  ...(ii)

On adding Eqs. (i) and (ii), we get

$\operatorname{ar}(\Delta B P Q)+\operatorname{ar}(\Delta O B Q)=\operatorname{ar}(\Delta B P S)+\operatorname{ar}(\Delta O B S)$

$\Rightarrow$ $\operatorname{ar}(\triangle P Q O)=\operatorname{ar}(\triangle P S O)$ Hence proved.