Obtain the equivalent capacitance of the network in Fig. 2.35.

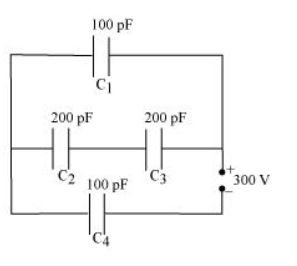
Capacitance of capacitor $C_{1}$ is $100 \mathrm{pF}$.

Capacitance of capacitor C2 is 200 pF.

Capacitance of capacitor C3 is 200 pF.

Capacitance of capacitor C4 is 100 pF.

Supply potential, V = 300 V

Capacitors $C_{2}$ and $C_{3}$ are connected in series. Let their equivalent capacitance be $C^{\prime}$.

$\therefore \frac{1}{C^{\prime}}=\frac{1}{200}+\frac{1}{200}=\frac{2}{200}$

$C^{\prime}=100 \mathrm{pF}$

Capacitors $C_{1}$ and $C$ ' are in parallel. Let their equivalent capacitance be $C^{\prime \prime}$.

$\therefore C^{\prime \prime}=C^{\prime}+\mathrm{C}_{1}$

$=100+100=200 \mathrm{pF}$

$C^{\prime \prime}$ and $C_{4}$ are connected in series. Let their equivalent capacitance be $C$.

$\therefore \frac{1}{C}=\frac{1}{C^{\prime \prime}}+\frac{1}{C_{4}}$

$=\frac{1}{200}+\frac{1}{100}=\frac{2+1}{200}$

$C=\frac{200}{3} \mathrm{pF}$

Hence, the equivalent capacitance of the circuit is $\frac{200}{3} \mathrm{pF}$.

Potential difference across $C^{\prime \prime}=V^{\prime \prime}$

Potential difference across $C_{4}=V_{4}$

$\therefore V^{\prime \prime}+V_{4}=V=300 \mathrm{~V}$

Charge on $C_{4}$ is given by,

$Q_{4}=C V$

$=\frac{200}{3} \times 10^{-12} \times 300$

$=2 \times 10^{-8} \mathrm{C}$

$\therefore V_{4}=\frac{Q_{4}}{C_{4}}$

$=\frac{2 \times 10^{-8}}{100 \times 10^{-12}}=200 \mathrm{~V}$

$\therefore$ Voltage across $C_{1}$ is given by,

$=300-200=100 \mathrm{~V}$$V_{1}=V-V_{4}$

Hence, potential difference, V1, across C1 is 100 V.

Charge on C1 is given by,

$Q_{1}=C_{1} V_{1}$

$=100 \times 10^{-12} \times 100$

$=10^{-8} \mathrm{C}$

C2 and C3 having same capacitances have a potential difference of 100 V together. Since C2 and C3 are in series, the potential difference across C2 and C3 is given by,

$V_{2}=V_{3}=50 \mathrm{~V}$

Therefore, charge on $C_{2}$ is given by,

$Q_{2}=C_{2} V_{2}$

$=200 \times 10^{-12} \times 50$

$=10^{-8} \mathrm{C}$

And charge on $C_{3}$ is given by,

$O_{2}=C, V_{2}$

$=200 \times 10^{-12} \times 50$

$=10^{-8} \mathrm{C}$

Hence, the equivalent capacitance of the given circuit is $\frac{200}{3} \mathrm{pF}$ with,