On a common hypotenuse AB, two right triangles ACB and ADB are situated on opposite sides.

Draw two right triangles ACB and ADB in a circle with centre O, where AB is the diameter of the circle.

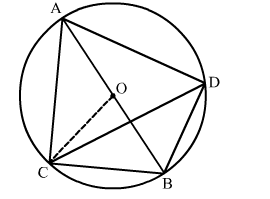
Join CO.

We know that the angle subtended by an arc of a circle at the centre is double the angle subtended by it on the remaining part of the circle.

Here, arc CB subtends ∠COB at the centre and ∠CAB at A on the circle.

∴ ∠COB = 2∠CAB           ...(1)

Also, arc CB subtends ∠COB at the centre and ∠CDB at D on the circle.

∴ ∠COB = 2∠CDB           ...(2)

Equating (1) and (2),
2∠CAB = 2∠CDB
⇒ ∠CAB = ∠CDB

Hence, ∠BAC = ∠BDC.