On a square cardboard sheet of area 784 cm2, four congruent circular plates of maximum size are placed such that each circular plate touches the
other two plates and each side of the square sheet is tangent to two circular plates. Find the area of the square sheet not covered by the circular plates.
$\because \quad$ Area of square $=784$
$\therefore \quad(\text { Side })^{2}=(28)^{2}$
$\Rightarrow \quad$ Side $=28 \mathrm{~cm}$
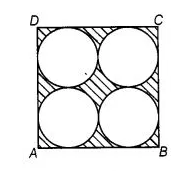
Since, all four are congruent circular plates.
$\therefore$ Diameter of each circular plate $=14 \mathrm{~cm}$
$\therefore$ Radius of each circular plate $=7 \mathrm{~cm}$
Now, area of one circular plate $=\pi r^{2}=\frac{22}{7}(7)^{2}$
$=154 \mathrm{~cm}^{2}$
$\therefore \quad$ Area of four circular plates $=4 \times 154=616 \mathrm{~cm}^{2}$
$\therefore$ Area of the square sheet not covered by the circular plates $=784-616=168 \mathrm{~cm}^{2}$