Question.
P and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
(i) $\operatorname{ar}($ PRQ $)=\frac{1}{2} \operatorname{ar}($ ARC $)$
(ii) $\operatorname{ar}(\mathrm{RQC})=\frac{3}{8} \operatorname{ar}(\mathrm{ABC})$
(iii) $\operatorname{ar}(\mathrm{PBQ})=\operatorname{ar}(\mathrm{ARC})$
(i) $\operatorname{ar}($ PRQ $)=\frac{1}{2} \operatorname{ar}($ ARC $)$
(ii) $\operatorname{ar}(\mathrm{RQC})=\frac{3}{8} \operatorname{ar}(\mathrm{ABC})$
(iii) $\operatorname{ar}(\mathrm{PBQ})=\operatorname{ar}(\mathrm{ARC})$
Solution:
Take a point $S$ on $A C$ such that $S$ is the mid-point of $A C$.
Extend $P Q$ to $T$ such that $P Q=Q T$.
Join TC, QS, PS, and AQ.
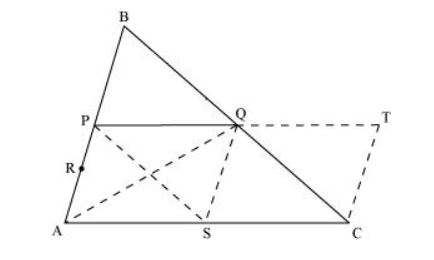
In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
$P Q \| A C$ and $P Q=\frac{1}{2} A C$
$\Rightarrow P Q \| A S$ and $P Q=A S(A s S$ is the mid-point of $A C)$
$\therefore$ PQSA is a parallelogram. We know that diagonals of a parallelogram bisect it into equal areas of triangles.
$\therefore \operatorname{ar}(\Delta \mathrm{PAS})=\operatorname{ar}(\Delta \mathrm{SQP})=\operatorname{ar}(\Delta \mathrm{PAQ})=\operatorname{ar}(\Delta \mathrm{SQA})$
Similarly, it can also be proved that quadrilaterals PSCQ, QSCT, and PSQB are also parallelograms and therefore,
ar (ΔPSQ) = ar (ΔCQS) (For parallelogram PSCQ)
ar (ΔQSC) = ar (ΔCTQ) (For parallelogram QSCT)
ar (ΔPSQ) = ar (ΔQBP) (For parallelogram PSQB)
Thus,
$\operatorname{ar}(\Delta \mathrm{PAS})=\operatorname{ar}(\Delta \mathrm{SQP})=\operatorname{ar}(\Delta \mathrm{PAQ})=\operatorname{ar}(\Delta \mathrm{SQA})=\operatorname{ar}(\Delta \mathrm{QSC})=\operatorname{ar}(\Delta \mathrm{CTQ})=\operatorname{ar}(\Delta \mathrm{QBP}) \ldots(1)$
Also, $\operatorname{ar}(\triangle \mathrm{ABC})=\operatorname{ar}(\triangle \mathrm{PBQ})+\operatorname{ar}(\triangle \mathrm{PAS})+\operatorname{ar}(\triangle \mathrm{PQS})+\operatorname{ar}(\triangle \mathrm{QSC})$
$\operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})$
$=\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})$
$=4 \operatorname{ar}(\Delta P B Q)$
$\Rightarrow \operatorname{ar}(\Delta \mathrm{PBQ})=\frac{1}{4} \operatorname{ar}(\triangle \mathrm{ABC}) \ldots(2)$
(i)Join point P to C.
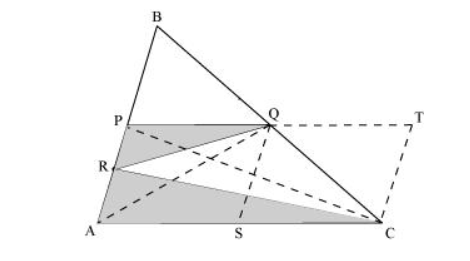
In $\triangle \mathrm{PAQ}, \mathrm{QR}$ is the median.
$\therefore \operatorname{ar}(\Delta \mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAQ})=\frac{1}{2} \times \frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC}) \ldots$(3)
In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
$P Q=\frac{1}{2} A C$
$\mathrm{AC}=2 \mathrm{PQ} \Rightarrow \mathrm{AC}=\mathrm{PT}$
Also, $P Q\|A C \Rightarrow P T\| A C$
Hence, PACT is a parallelogram.
$\operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\mathrm{PACQ})+\operatorname{ar}(\Delta \mathrm{QTC})$
$=\operatorname{ar}(\mathrm{PACQ})+\operatorname{ar}(\Delta \mathrm{PBQ}[\cup \operatorname{sing}$ equation $(1)]$
$\therefore \operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\triangle \mathrm{ABC}) \ldots$(4)
$\operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAC})$
(CR is the median of $\triangle \mathrm{PAC}$ )
$=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(\mathrm{PACT})(\mathrm{PC}$ is the diagonal of parallelogram $\mathrm{PACT})$'
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{PACT})=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})$
$\Rightarrow \frac{1}{2} \operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC})$
$\Rightarrow \frac{1}{2} \operatorname{ar}(\Delta \mathrm{ARC})=\operatorname{ar}(\Delta \mathrm{PRQ})$ [Using equation (3)]..(5)
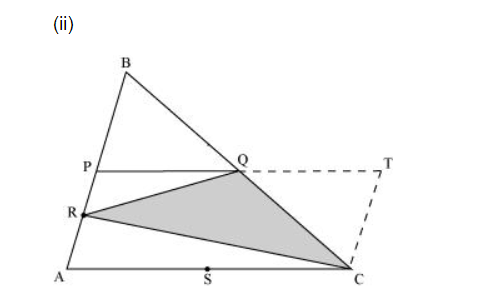
$\operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\Delta \mathrm{PRQ})+\operatorname{ar}(\Delta \mathrm{ARC})+\operatorname{ar}(\Delta \mathrm{QTC})+\operatorname{ar}(\Delta \mathrm{RQC})$
Putting the values from equations (1), (2), (3), (4), and (5), we obtain
$\operatorname{ar}(\Delta \mathrm{ABC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC})+\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})+\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})+\operatorname{ar}(\Delta \mathrm{RQC})$
$\operatorname{ar}(\triangle \mathrm{ABC})=\frac{5}{8} \operatorname{ar}(\triangle \mathrm{ABC})+\operatorname{ar}(\triangle \mathrm{RQC})$
$\operatorname{ar}(\Delta \mathrm{RQC})=\left(1-\frac{5}{8}\right) \operatorname{ar}(\Delta \mathrm{ABC})$
$\operatorname{ar}(\Delta R Q C)=\frac{3}{8} \operatorname{ar}(\Delta A B C)$
(iii) In parallelogram PACT,
$\operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAC})$
(CR is the median of $\triangle \mathrm{PAC}$ )
$=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(\mathrm{PACT})(\mathrm{PC}$ is the diagonal of parallelogram $\mathrm{PACT})$
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{PACT})$
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})$
$=\operatorname{ar}(\Delta \mathrm{PBQ})$
Take a point $S$ on $A C$ such that $S$ is the mid-point of $A C$.
Extend $P Q$ to $T$ such that $P Q=Q T$.
Join TC, QS, PS, and AQ.

In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
$P Q \| A C$ and $P Q=\frac{1}{2} A C$
$\Rightarrow P Q \| A S$ and $P Q=A S(A s S$ is the mid-point of $A C)$
$\therefore$ PQSA is a parallelogram. We know that diagonals of a parallelogram bisect it into equal areas of triangles.
$\therefore \operatorname{ar}(\Delta \mathrm{PAS})=\operatorname{ar}(\Delta \mathrm{SQP})=\operatorname{ar}(\Delta \mathrm{PAQ})=\operatorname{ar}(\Delta \mathrm{SQA})$
Similarly, it can also be proved that quadrilaterals PSCQ, QSCT, and PSQB are also parallelograms and therefore,
ar (ΔPSQ) = ar (ΔCQS) (For parallelogram PSCQ)
ar (ΔQSC) = ar (ΔCTQ) (For parallelogram QSCT)
ar (ΔPSQ) = ar (ΔQBP) (For parallelogram PSQB)
Thus,
$\operatorname{ar}(\Delta \mathrm{PAS})=\operatorname{ar}(\Delta \mathrm{SQP})=\operatorname{ar}(\Delta \mathrm{PAQ})=\operatorname{ar}(\Delta \mathrm{SQA})=\operatorname{ar}(\Delta \mathrm{QSC})=\operatorname{ar}(\Delta \mathrm{CTQ})=\operatorname{ar}(\Delta \mathrm{QBP}) \ldots(1)$
Also, $\operatorname{ar}(\triangle \mathrm{ABC})=\operatorname{ar}(\triangle \mathrm{PBQ})+\operatorname{ar}(\triangle \mathrm{PAS})+\operatorname{ar}(\triangle \mathrm{PQS})+\operatorname{ar}(\triangle \mathrm{QSC})$
$\operatorname{ar}(\Delta \mathrm{ABC})=\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})$
$=\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})+\operatorname{ar}(\Delta \mathrm{PBQ})$
$=4 \operatorname{ar}(\Delta P B Q)$
$\Rightarrow \operatorname{ar}(\Delta \mathrm{PBQ})=\frac{1}{4} \operatorname{ar}(\triangle \mathrm{ABC}) \ldots(2)$
(i)Join point P to C.

In $\triangle \mathrm{PAQ}, \mathrm{QR}$ is the median.
$\therefore \operatorname{ar}(\Delta \mathrm{PRQ})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAQ})=\frac{1}{2} \times \frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC}) \ldots$(3)
In ΔABC, P and Q are the mid-points of AB and BC respectively. Hence, by using mid-point theorem, we obtain
$P Q=\frac{1}{2} A C$
$\mathrm{AC}=2 \mathrm{PQ} \Rightarrow \mathrm{AC}=\mathrm{PT}$
Also, $P Q\|A C \Rightarrow P T\| A C$
Hence, PACT is a parallelogram.
$\operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\mathrm{PACQ})+\operatorname{ar}(\Delta \mathrm{QTC})$
$=\operatorname{ar}(\mathrm{PACQ})+\operatorname{ar}(\Delta \mathrm{PBQ}[\cup \operatorname{sing}$ equation $(1)]$
$\therefore \operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\triangle \mathrm{ABC}) \ldots$(4)
$\operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAC})$
(CR is the median of $\triangle \mathrm{PAC}$ )
$=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(\mathrm{PACT})(\mathrm{PC}$ is the diagonal of parallelogram $\mathrm{PACT})$'
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{PACT})=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})$
$\Rightarrow \frac{1}{2} \operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC})$
$\Rightarrow \frac{1}{2} \operatorname{ar}(\Delta \mathrm{ARC})=\operatorname{ar}(\Delta \mathrm{PRQ})$ [Using equation (3)]..(5)

$\operatorname{ar}(\mathrm{PACT})=\operatorname{ar}(\Delta \mathrm{PRQ})+\operatorname{ar}(\Delta \mathrm{ARC})+\operatorname{ar}(\Delta \mathrm{QTC})+\operatorname{ar}(\Delta \mathrm{RQC})$
Putting the values from equations (1), (2), (3), (4), and (5), we obtain
$\operatorname{ar}(\Delta \mathrm{ABC})=\frac{1}{8} \operatorname{ar}(\Delta \mathrm{ABC})+\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})+\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})+\operatorname{ar}(\Delta \mathrm{RQC})$
$\operatorname{ar}(\triangle \mathrm{ABC})=\frac{5}{8} \operatorname{ar}(\triangle \mathrm{ABC})+\operatorname{ar}(\triangle \mathrm{RQC})$
$\operatorname{ar}(\Delta \mathrm{RQC})=\left(1-\frac{5}{8}\right) \operatorname{ar}(\Delta \mathrm{ABC})$
$\operatorname{ar}(\Delta R Q C)=\frac{3}{8} \operatorname{ar}(\Delta A B C)$
(iii) In parallelogram PACT,
$\operatorname{ar}(\Delta \mathrm{ARC})=\frac{1}{2} \operatorname{ar}(\Delta \mathrm{PAC})$
(CR is the median of $\triangle \mathrm{PAC}$ )
$=\frac{1}{2} \times \frac{1}{2} \operatorname{ar}(\mathrm{PACT})(\mathrm{PC}$ is the diagonal of parallelogram $\mathrm{PACT})$
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{PACT})$
$=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC})$
$=\operatorname{ar}(\Delta \mathrm{PBQ})$
