Question:
P is a point on the bisector of ∠ABC. If the line through P, parallel to BA meet BC at Q, prove that BPQ is an isosceles triangle.
Solution:
Given we have P is a point on the bisector of ∠ABC and draw the line through P parallel to BA and meet BC at Q.
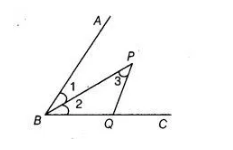
To prove $\triangle B P Q$ is an isosceles triangle.
Proof $\angle 1=\angle 2$ $[\because B P$ is bisector of $\angle B$ (given)]
Now, $\angle 1=\angle 3$ [alternate interior angles as $P Q \| A B$ ]
$\therefore$ $\angle 2=\angle 3$
$\Rightarrow$ $P Q=B Q \quad$ [sides opposite to equal angles are equal]
Hence, $\triangle B P Q$ is an isosceles triangle.
Hence proved.