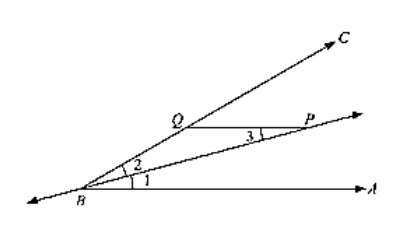
P is a point on the bisector of an angle ABC. If the line through P parallel to AB meets BC at Q, prove that triangle BPQ is isosceles.

Solution:

Given that P is a point on the bisector of an angle ABC, and PQ ∥ AB.

We have to prove that ΔBPQ is isosceles.

Since,

BP is bisector of ∠ABC = ∠ABP = ∠PBC .... (i)

Now,

PQ ∥ AB

∠BPQ = ∠ABP ... (ii) [alternative angles]

From (i) and (ii), we get

∠BPQ = ∠PBC (or) ∠BPQ = ∠PBQ

Now,

In BPQ,

∠BPQ = ∠PBQ

ΔBPQ is an isosceles triangle.

Hence proved