P, Q, R and S are respectively the mid-points

Solution:

Given In quadrilateral ABCD, P, O, S and S are the mid-points of the sides AB, BC, CD and DA, respectively.

Also, AC ⊥ BD

To prove PQRS is a rectangle.

Proof Since, AC ⊥ BD .

∠COD = ∠AOD= ∠AOB= ∠COB = 90°

In $\triangle A D C, S$ and $R$ are the mid-points of $A D$ and $D C$ respectively, then by mid-point theorem

$S R \| A C$ and $S R=\frac{1}{2} A C$ ....(i)

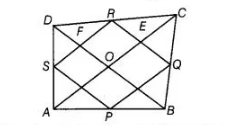
In $\triangle A B C, P$ and $Q$ are the mid-points of $A B$ and $B C$ respectively, then by mid-point theorem

$P Q \| A C$ and $P Q=\frac{1}{2} A C$ ...(ii)

 From Eqs. (i) and (ii), $P Q \| S R$ and $P Q=S R=\frac{1}{2} A C$....(iii)

Similarty, $S P \| R Q$ and $S P=R Q=\frac{1}{2} B D$  ....(iv)

Now, in quadrilateral EOFR,    $O E\|F R, O F\| E R$

$\therefore$ $\angle E O F=\angle E R F=90^{\circ}\left[\because \angle C O D=90^{\circ} \Rightarrow \angle E O F=90^{\circ}\right] \ldots(\mathrm{V})$

So, $P Q R S$ is a rectangle.

Hence proved.