Question:
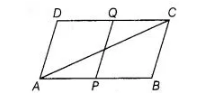
Points P and Q have been taken on opposite sides AB and CD, respectively of a parallelogram ABCD such that AP = CQ. Show that AC and PQ bisect each other.
Solution:
Given $A B C D$ is a parallelogram and $A P=C Q$
To show $A C$ and $P Q$ bisect each other.
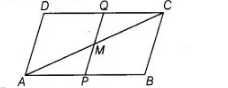
Proof In $\triangle A M P$ and $\Delta C M Q$,
$\angle M A P=\angle M C Q$ [alternate interior angles]
$A P=C Q$ [given]
and $\angle A P M=\angle C Q M$ [alternate interior angles]
$\therefore$ $\triangle A M P \cong \triangle C M Q$ [by ASA congruence rule]
$\Rightarrow$ $A M=C M$ [by CPCT rule]
Hence, $A C$ and $P Q$ bisect each other.
Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
