Question:
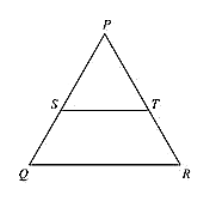
PQR is a triangle in which PQ = PR and is any point on the side PQ. Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS = PT.
Solution:
Given that PQR is a triangle such that PQ = PR ant S is any point on the side PQ and ST ∥ QR.
To Prove,
PS = PT
Since, PQ = PR
PQR is an isosceles triangle.
∠Q = ∠R (or) ∠PQR = ∠PRQ
Now, ∠PST = ∠PQR and ∠PTS = ∠PRQ [Corresponding angles as ST parallel to QR]
Since, ∠PQR = ∠PRQ
∠PST = ∠PTS
Now, In ΔPST, ∠PST = ∠PTS
ΔPST is an isosceles triangle
Therefore, PS = PT
