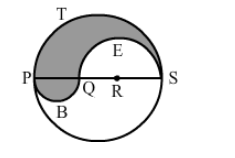
PQRS is a diameter of a circle of radius 6 cm. The lengths PQ, QR and RS are equal. Semicircles are drawn with PQ and QS as diameters, as shown in the given figure. If PS = 12 cm, find the perimeter and area of the shaded region.
Perimeter (circumference of the circle) $=2 \pi \mathrm{r}$
We know:
Perimeter of a semicircular $\operatorname{arc}=\pi \mathrm{r}$
Now,
For the arc PTS, radius is 6 cm.
$\therefore$ Circumference of the semicircle PTS $=\pi \mathrm{r}=6 \pi \mathrm{cm}$
For the arc QES, radius is 4 cm.
$\therefore$ Circumference of the semicircle $Q E S=\pi r=4 \pi \mathrm{cm}$
For the arc PBQ, radius is 2 cm.
$\therefore$ Circumference of the semicircle $\mathrm{PBQ}=\pi \mathrm{r}=2 \pi \mathrm{cm}$
Now,
Perimeter of the shaded region $=6 \pi+4 \pi+2 \pi$
$=12 \pi \mathrm{cm}$
$=12 \times 3.14$
$=37.68 \mathrm{~cm}$
Area of the semicircle $P B Q=\frac{1}{2} \pi r^{2}$
$=\frac{1}{2} \times 3.14 \times 6 \times 6$
$=56.52 \mathrm{~cm}^{2}$
Area of the semicircle $\mathrm{QES}=\frac{1}{2} \pi \mathrm{r}^{2}$
$=\frac{1}{2} \times 3.14 \times 4 \times 4$
$=25.12 \mathrm{~cm}^{2}$
Area of the shaded region = Area of the semicircle PBQ + Area of the semicircle PTS
$=6.28+56.52-25.12=37.68 \mathrm{~cm}^{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
