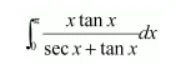
Let $I=\int_{0}^{\pi} \frac{x \tan x}{\sec x+\tan x} d x$ ...(1)
$I=\int_{0}^{\pi}\left\{\frac{(\pi-x) \tan (\pi-x)}{\sec (\pi-x)+\tan (\pi-x)}\right\} d x$ $\left(\int_{0}^{0} f(x) d x=\int_{0}^{a} f(a-x) d x\right)$
$\Rightarrow I=\int_{0}^{\pi}\left\{\frac{-(\pi-x) \tan x}{-(\sec x+\tan x)}\right\} d x$
$\Rightarrow I=\int_{0}^{\pi} \frac{(\pi-x) \tan x}{\sec x+\tan x} d x$ ...(2)
Adding (1) and (2), we obtain
$2 I=\int_{0}^{\pi} \frac{\pi \tan x}{\sec x+\tan x} d x$
$\Rightarrow 2 I=\pi \int_{0}^{\pi} \frac{\frac{\sin x}{\cos x}}{\frac{1}{\cos x}+\frac{\sin x}{\cos x}} d x$
$\Rightarrow 2 I=\pi \int_{0}^{\pi} \frac{\sin x+1-1}{1+\sin x} d x$
$\Rightarrow 2 I=\pi \int_{0}^{\pi} 1 \cdot d x-\pi \int_{0}^{\pi} \frac{1}{1+\sin x} d x$
$\Rightarrow 2 I=\pi[x]_{0}^{\pi}-\pi \int_{0}^{\pi} \frac{1-\sin x}{\cos ^{2} x} d x$
$\Rightarrow 2 I=\pi^{2}-\pi \int_{0}^{\pi}\left(\sec ^{2} x-\tan x \sec x\right) d x$
$\Rightarrow 2 I=\pi^{2}-\pi[\tan x-\sec x]_{0}^{\pi}$
$\Rightarrow 2 I=\pi^{2}-\pi[\tan \pi-\sec \pi-\tan 0+\sec 0]$
$\Rightarrow 2 I=\pi^{2}-\pi[0-(-1)-0+1]$
$\Rightarrow 2 I=\pi^{2}-2 \pi$
$\Rightarrow 2 I=\pi(\pi-2)$
$\Rightarrow I=\frac{\pi}{2}(\pi-2)$
