Let $A=\{-1,0,1,2\}$ and $B=\{2,3,4,5\}$. Find which of the following are function from A to B. Give reason.
(i) $f=\{(-1,2),(-1,3),(0,4), 1,5)\}$
(ii) $g=\{(0,2),(1,3),(2,4)\}$
(iii) $h=\{(-1,2),(0,3),(1,4),(2,5)\}$
(i) Given: $A=\{-1,0,1,2\}$ and $B=\{2,3,4,5\}$
Function:
(i) all elements of the first set are associated with the elements of the second set.
(ii) An element of the first set has a unique image in the second set.
$f=\{(-1,2),(-1,3),(0,4),(1,5)\}$
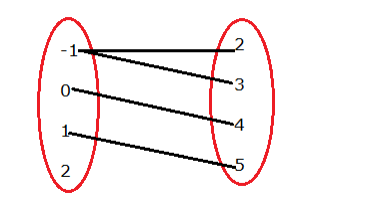
$f=\{(-1), 2),(-1), 3),(0,4),(1,5)\}$
Here, -1 is coming twice.
Hence, it does not have a unique (one) image.
∴ f is not a function
(ii) Given: $A=\{-1,0,1,2\}$ and $B=\{2,3,4,5\}$
Function:
(i) all elements of first set is associated with the elements of second set.
(ii) An element of first set has a unique image in second set.
$g=\{(0,2),(1,3),(2,4)\}$
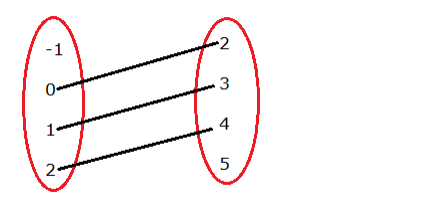
Here, -1 is not associated with any element of set B
Hence, it does not satisfy the condition of the function
∴ g is not a function.
(iii) Given: $A=\{-1,0,1,2\}$ and $B=\{2,3,4,5\}$
Function:
(i) all elements of first set is associated with the elements of second set.
(ii) An element of first set has a unique image in second set.
$h=\{(-1,2),(0,3),(1,4),(2,5)\}$
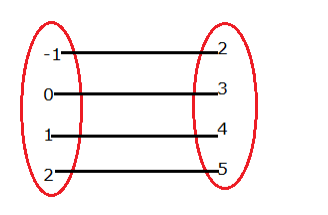
Here, (i) all elements of set A are associated to element in set B.
(ii) an element of set A is associated to a unique element in set B
∴ h is a function.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
