Prove that:

Solution:

(i) We have to prove that $\frac{\sqrt{3 \times 5^{-3}}}{\sqrt[3]{3^{-1} \sqrt{5}}} \times \sqrt[6]{3 \times 5^{6}}=\frac{3}{5}$

By using rational exponent $a^{-n}=\frac{1}{a^{n}}$ we get,

$\frac{\sqrt{3 \times 5^{-3}}}{\sqrt[3]{3^{-1} \sqrt{5}}} \times \sqrt[6]{3 \times 5^{6}}=\frac{\sqrt{3 \times \frac{1}{5^{3}}}}{\sqrt[3]{\frac{1}{3}} \sqrt{5}} \times \sqrt[6]{3 \times 5^{6}}$

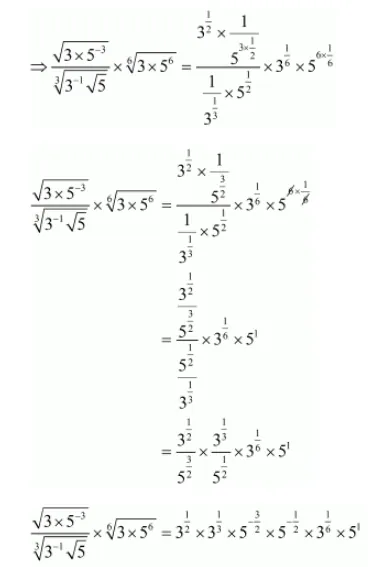
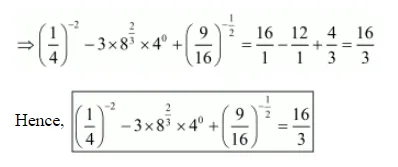
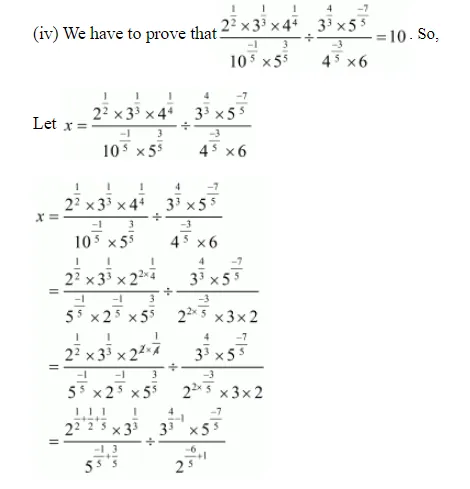
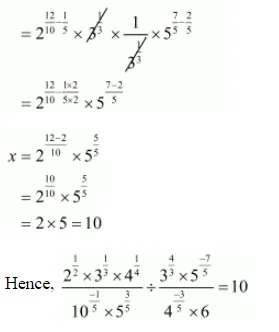
(v) We have to prove that $\sqrt{\frac{1}{4}}+(0.01)^{\frac{-1}{2}}-(27)^{\frac{2}{3}}=\frac{3}{2}$

Let $x=\sqrt{\frac{1}{4}}+(0.01)^{\frac{-1}{2}}-(27)^{\frac{2}{3}}$

$x=\sqrt{\frac{1}{4}}+(0.01)^{\frac{-1}{2}}-(27)^{\frac{2}{3}}$

$=\sqrt{\frac{1}{2^{2}}}+\left(\frac{0.01 \times 100}{1 \times 100}\right)^{\frac{-1}{2}}-\left(3^{3}\right)^{\frac{2}{3}}$

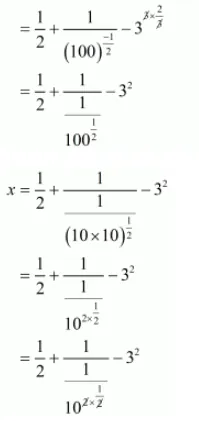
$x=\frac{1}{2}+\frac{1}{\frac{1}{10}}-3^{2}$

$=\frac{1}{2}+1 \times \frac{10}{1}-3 \times 3$

$=\frac{1}{2}+10-9$

$=\frac{3}{2}$

Hence, $\sqrt{\frac{1}{4}}+(0.01)^{\frac{-1}{2}}-(27)^{\frac{2}{3}}=\frac{3}{2}$

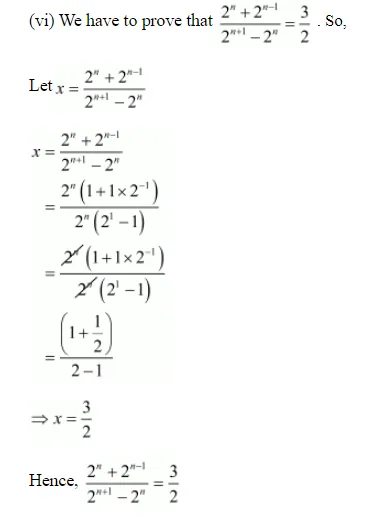
(vii) We have to prove that $\left(\frac{64}{125}\right)^{\frac{-2}{3}}+\frac{1}{\left(\frac{256}{625}\right)^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{\sqrt[3]{64}}\right)=\frac{65}{16}$. So let

$x=\left(\frac{64}{125}\right)^{\frac{-2}{3}}+\frac{1}{\left(\frac{256}{625}\right)^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{\sqrt[3]{64}}\right)$

$x=\frac{2^{6 \times \frac{2}{3}}}{5^{3 \times \frac{-2}{3}}}+\frac{1}{\frac{2^{8 \times \frac{1}{4}}}{5^{4 \times \frac{1}{4}}}}+\frac{\sqrt{5 \times 5}}{\sqrt[3]{4 \times 4 \times 4}}$

By taking least common factor we get 

$x=\frac{25+20+20}{16}=\frac{65}{16}=\frac{65}{16}$

Hence, $\left(\frac{64}{125}\right)^{\frac{-2}{3}}+\frac{1}{\left(\frac{256}{625}\right)^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{3 \sqrt{64}}\right)=\frac{65}{16}$

(viii) We have to prove that $\frac{3^{-3} \times 6^{2} \times \sqrt{98}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{\frac{-4}{3}} \times 3^{\frac{1}{3}}}=28 \sqrt{2}$. So,

Let $x=\frac{3^{-3} \times 6^{2} \times \sqrt{98}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{\frac{-4}{3}} \times 3^{\frac{1}{3}}}$

$x=\frac{3^{-3} \times 6^{2} \times \sqrt{98}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{\frac{-4}{3}} \times 3^{\frac{1}{3}}}$

$=\frac{3^{-3} \times 3^{2} \times 2^{2} \times \sqrt{7 \times 7 \times 2}}{5^{2} \times \sqrt[3]{\frac{1}{25}} \times(15)^{\frac{-4}{3}} \times 3^{\frac{1}{3}}}$

$=\frac{3^{-3+2} \times 2^{2} \times 7 \sqrt{2}}{5^{2} \times \frac{1}{5^{2 \times \frac{1}{3}}} \times 5^{\frac{4}{3}} \times 3^{\frac{4}{3}} \times 3^{\frac{1}{3}}}$

$x=\frac{3^{-1} \times 2^{2} \times 7 \sqrt{2}}{\frac{5^{2}}{1} \times \frac{1}{5^{\frac{2}{3}}} \times \frac{1}{5^{\frac{4}{3}}} \times \frac{1}{3^{\frac{4}{3}}} \times \frac{3^{\frac{1}{3}}}{1}}$

$=3^{-1} \times 2^{2} \times 7 \sqrt{2} \times \frac{1}{5^{2}} \times 5^{\frac{2}{3}} \times 5^{\frac{4}{3}} \times 3^{\frac{4}{3}} \times \frac{1}{3^{\frac{1}{3}}}$

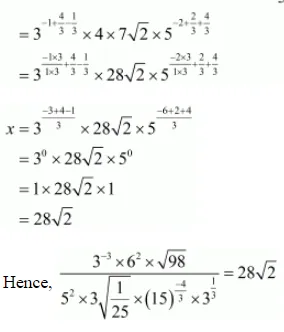
(ix) We have to prove that $\frac{(0.6) 0-(0.1)^{-1}}{\left(\frac{3}{8}\right)^{-1}\left(\frac{3}{2}\right)^{3}+\left(\frac{-1}{3}\right)^{-1}}=\frac{-3}{2}$. So,

Let $x=\frac{(0.6) 0-(0.1)^{-1}}{\left(\frac{3}{8}\right)^{-1}\left(\frac{3}{2}\right)^{3}+\left(\frac{-1}{3}\right)^{-1}}$

$x=\frac{1-\left(\frac{0.1 \times 10}{1 \times 10}\right)^{-1}}{\left(\frac{3^{-1}}{2^{3 x-1}}\right)\left(\frac{3^{3}}{2^{3}}\right)+\left(\frac{-1^{-1}}{3^{-1}}\right)}$

$=\frac{1-\frac{1}{10^{-1}}}{\left(\frac{3^{-1}}{2^{-3}}\right)\left(\frac{3^{3}}{2^{3}}\right)+\left(\frac{-1}{\frac{1}{3^{1}}}\right)}$

$=\frac{1-\frac{1}{\frac{1}{10}}}{\frac{3^{-1+3}}{2^{-3+3}}+\left(-1 \times \frac{3}{1}\right)}$

$=\frac{1-1 \times 10}{\frac{3^{2}}{2^{0}}+(-3)}$

$\Rightarrow x=\frac{1-10}{\frac{3^{2}}{1}-3}=\frac{-9}{9-3}=-\frac{3}{2}$

Hence, $\frac{(0.6) 0-(0.1)^{-1}}{\left(\frac{3}{8}\right)^{-1}\left(\frac{3}{2}\right)^{3}+\left(\frac{-1}{3}\right)^{-1}}=-\frac{3}{2}$