Prove that, if a line is drawn parallel to

Let a ΔABC in which a line DE parallel to SC intersects AB at D and AC at E.To prove DE divides the two sides in the same ratio.

i.e., $\frac{A D}{D B}=\frac{A E}{E C}$

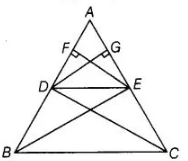
Construction Join $B E, C D$ and draw $E F \perp A B$ and $D G \perp A C$.

Proof Here, $\frac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta B D E)}=\frac{\frac{1}{2} \times A D \times E F}{\frac{1}{2} \times D B \times E F}$

$\left[\because\right.$ area of triangle $=\frac{1}{2} \times$ base $\times$ height $]$

$=\frac{A D}{D B}$ .....(i)

similarly, $\frac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta D E C)}=\frac{\frac{1}{2} \times A E \times G D}{\frac{1}{2} \times E C \times G D}=\frac{A E}{E C}$.....(ii)

Now, since, $\triangle B D E$ and $\triangle D E C$ lie between the same parallel $D E$ and $B C$ and on the same base $D E$

So, $\operatorname{ar}(\Delta B D E)=\operatorname{ar}(\triangle D E C)$ ....(iii)

From Eqs. (i), (ii) and (iii), 

$\frac{A D}{D B}=\frac{A E}{E C}$\

Hence proved.